锁定候选法（Locked Candidates）

核心概念

锁定候选也被称为交叉消除（Intersection Removal）。当一个数字在某一宫的某一行/列中只能有特定放置位置时，就可以在交叉的区域进行消除。该技巧有两种子类型：行列区块对宫排除/宣称法（类型 2）和宫区块对行列排除/指向法（类型 1）。

锁定候选法类型 1：宫区块对行列排除/指向法

当一个数字在一个宫内被限制到某一行或某一列时，它会同时排除该行/列中宫外的同一数字的可能性。

示例 1

在第 1 宫（B1，左上角 3×3 宫）里，数字 5 的候选只可能出现在第 3 行。具体来说，它只在 R3C1 和 R3C2 这两个格子里出现。
因为 5 必须落在 B1 的这两个格子之一，那么 在第 3 行的其它宫里（比如 R3C7）就不可能再有 5 了。所以，可以把 R3C7 的候选 5 删除。

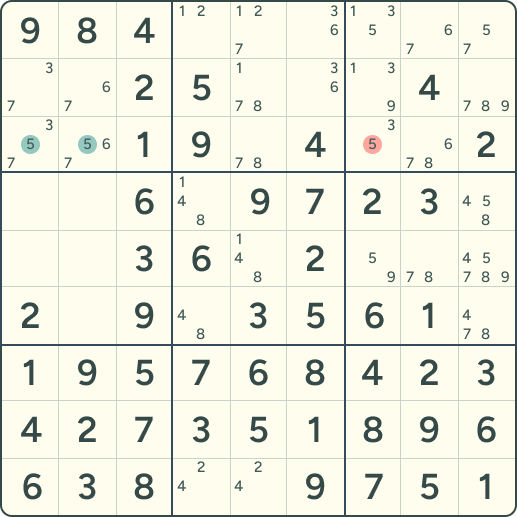
示例 2

在第 8 宫（B8，底部中间的 3×3 宫）里，数字 1 的所有候选位置都集中在第 7 行。这意味着，1 在 B8 必须落在 R7 的这些格子之一。因此，在 第 7 行与 B8 相交的其它宫（B7 和 B9）中，R7 的那些格子就不可能是 1。这样一来，在 R7 的交叠宫（B7 和 B9）的格子中，可以一次性消掉最多 6 个候选“1”。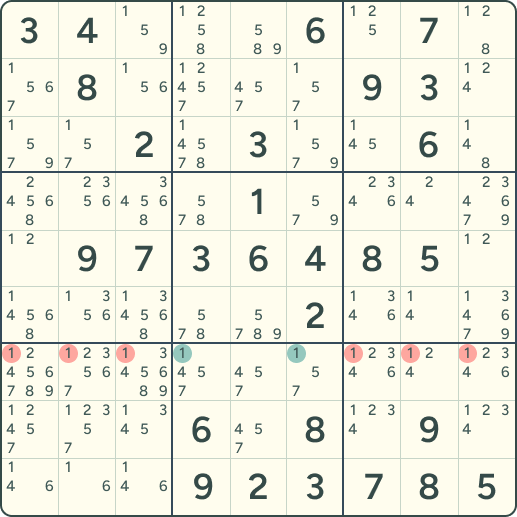

锁定候选法类型 2：行列区块对宫排除/宣称法

一旦某数字的候选沿某一行或某一列被限定在同一宫内，它将在该宫的其他格子中被排除。

示例 1 :

1. 在第 1 宫（B1，左上角 3×3 宫）里，数字 7 的候选只可能出现在 第 1 列和第 3 列。也就是说，7 在 B1 只能落在 C1 或 C3 上。
2. 因此，B1 内但在 第 2 列（C2） 的格子（比如 R3C2）就 不可能是 7。所以，可以把 R3C2 的候选 7 删除。

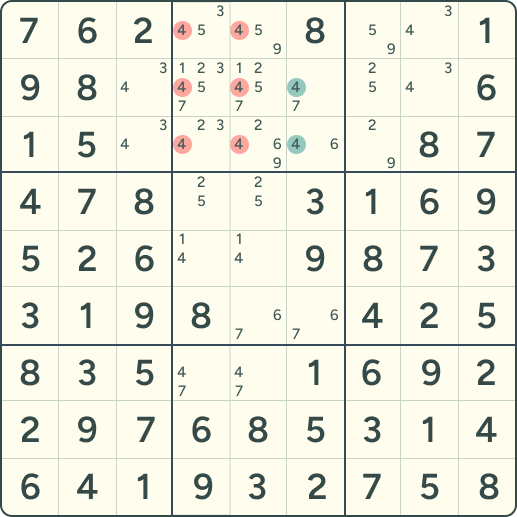
示例 2 :

1. 在第 6 列（C6）中，数字 4 的所有候选位置都被限制在同一个九宫格 B2 内；
2. 因此在宫 B2 的其它格子里可以把 “4” 的候选全部去掉。