隐性数对(Hidden Pairs)
识别隐性数对
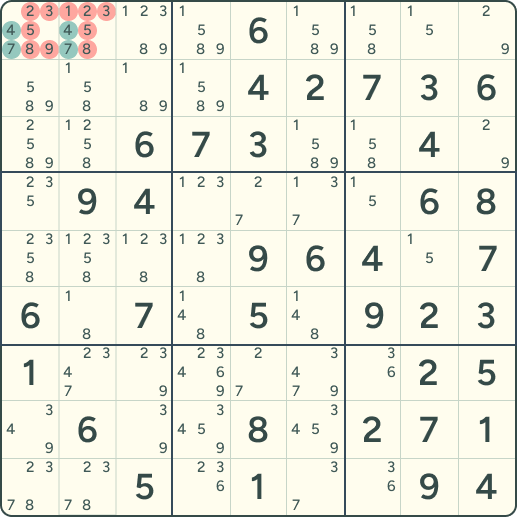
当在棋盘上把候选数字(铅笔记号)标出来并显现时,隐性数对就会变得可见。例如,当在已标注候选的格子中标出数字 4 与 8 后,格子 R3C4 与 R3C6 会呈现出这样的候选关系,从而直观上让人认为这些格子不再适合填入其他数字。
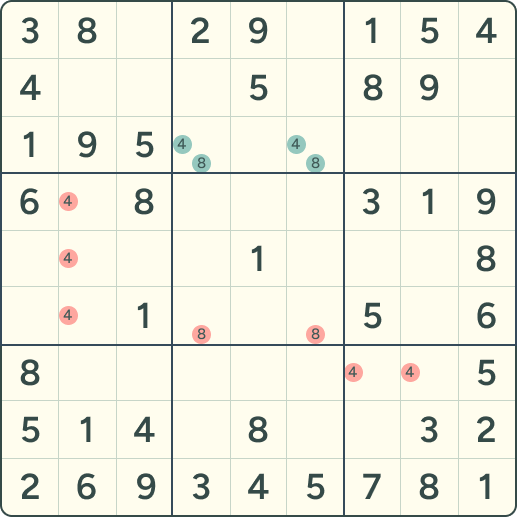
隐性子集与显性子集的比较
跟踪多个格子里的候选可能会很复杂,需要较强的模式识别能力,尤其是在更大的隐性子集(如隐性三数组、隐性四数组)中。由于解法在很大程度上依赖个人习惯,很多人会把所有可能性都标出来以便观察组合,因此更倾向于使用显性子集(即在候选中直观能看见的组合)。
隐性数对如何起作用
隐性数对发生在某一宫或单位(house)内:当两个候选数字只能被分配到该单位内的两个格子时,其他格子中这些数字的候选就可以被去除,从而把这两个格子“锁定”为那对数字(顺序未定)。示例 1(第 9 列):
在第 9 列里,只有 R5C9 和 R7C9 这两个格子包含候选 1 与 9,说明在这一列中 1 和 9 必定占据这两格(顺序未知)。既然如此,这两个格子里除了 1 与 9 外的其它候选就不可能成立,可以把它们删除(例如从 R5C9 删除候选 6)。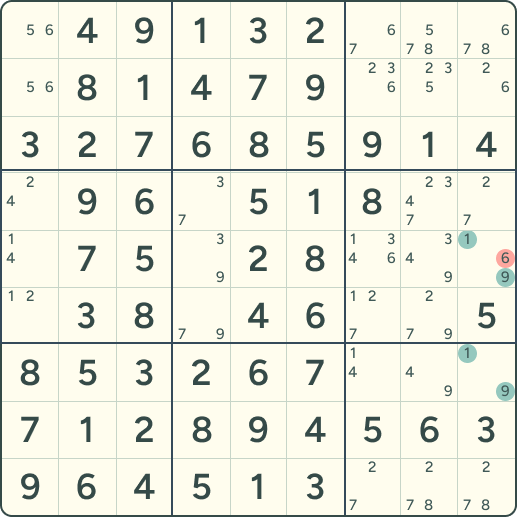
示例 2(第 1 行 / 第 1 宫):
在第 1 行(或第 1 宫)里,R1C1 与 R1C2 这两个格子虽然有很多铅笔记号,但在该行/该宫中只有数字 4 与 7 必须出现在这两个格子里(它们在该单位中只出现在这两格)。因此,可以把这两个格子中除 4 与 7 外的所有候选全部清除,使这两格最终只剩下候选 {4,7}。